語のメモ seqintra meeting (TOM/SAM, sudry, pvalue,refseq,ガンマ分布 etc.

general translocase of the outer membrane (TOM complex) and the sorting and assembly machinery (SAM complex), which is dedicated to β-barrel proteins. The SAM_core complex consists of three subunits, Sam35, Sam37, and Sam50, that can associate with a fourth subunit, the morphology component Mdm10, to form the SAM_holo complex.
by http://www.jbc.org/content/281/32/22819.full

sundry 【形】

いろいろな、種々｛しゅじゅ｝の、種々｛しゅじゅ｝さまざまな、いくつかの、数人｛すうにん｝ 

by eijiro

p値

【仮名】pち
【原文】p-value

統計用語。ある実験中に群間差が偶然生じる可能性を示す尺度。例えば、p値が0.01（p=0.01）というのは、この結果を偶然生じることが100回に1回あることを意味する。p値が小さくなるほど、それだけ群間差は治療により生じている可能性が高くなる。

by PDQ®がん用語辞書

有意確率 p value

統計的仮説検定において，帰無仮説のもとで得られた検定統計量が実現する確率。例えば，正規分布において標準得点が 1.96 以上となる確率は 2.5%。有意確率がまえもって定めた有意水準より小さい場合に帰無仮説を棄却し，大きい場合に帰無仮説を採択する。

by 統計学用語辞典


NCBI Reference Sequences The Reference Sequence (RefSeq) collection aims to provide a comprehensive, integrated, non-redundant, well-annotated set of sequences, including genomic DNA, transcripts, and proteins. RefSeq is a foundation for medical, functional, and diversity studies; they provide a stable reference for genome annotation, gene identification and characterization, mutation and polymorphism analysis (especially RefSeqGene records), expression studies, and comparative analyses.
by http://www.ncbi.nlm.nih.gov/RefSeq/

by統計学用語辞典

ガンマ分布

Excel にはgammadist，gammainvという関数が用意されている。


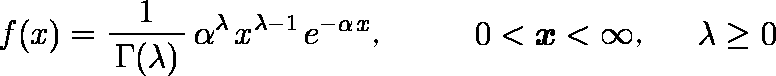
Γ ( λ ) はガンマ関数である。

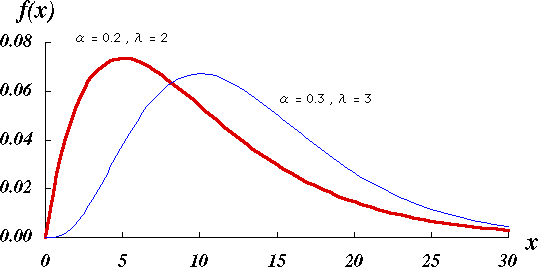図 1．ガンマ分布の概形

この分布で，λ = 1 すなわち，Γ ( 1， α ) は，f ( x ) = α e ^{- α x} となり，これは指数分布である。
平均 E ( x ) ，分散 V ( x ) は
E ( x ) = λ / α，　V ( x ) = λ / α²
である。

ガンマ分布

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2010/10/25 18:58 UTC 版)

確率論および統計学において、ガンマ分布 (gamma distribution) は連続確率分布の一種である。ガンマ分布の確率密度関数は、ガンマ関数を用いて次のように表される。

ここで、ガンマ分布の形状母数 k > 0、尺度母数 θ > 0 である。
ガンマ分布の累積分布関数は、不完全ガンマ関数を用いて次のように表される。

ガンマ分布の確率変数を X とするとき、平均 E(X) および分散 V(X) は次のように表される。

ガンマ分布は再生性を有する。すなわち、パラメータに k₁ と θ を持つガンマ分布の確率変数を X₁、パラメータに k₂ と θ を持つガンマ分布の確率変数を X₂ とするとき、確率変数が X₁ + X₂ であるガンマ分布のパラメータは k₁ + k₂ と θ である。
k が整数である場合、このガンマ分布はアーラン分布となる。特にk = 1 である場合、このガンマ分布はパラメータに θ を持つ指数分布となる。また、パラメータに θ を持つ互いに独立な n 個の指数分布の和は、パラメータに n と θ を持つガンマ分布（アーラン分布）となる。
k が半整数であり、かつ θ = 2 である場合、ガンマ分布はカイ二乗分布となる。